Description
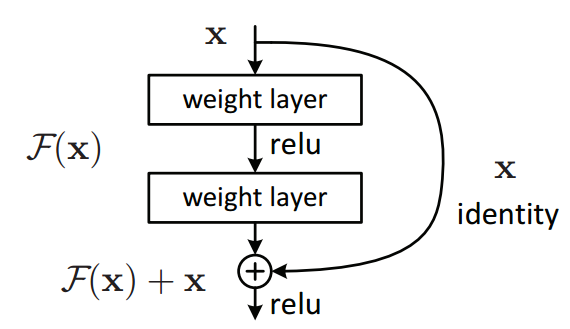
This is a residual block, or skip connection. The residual is the difference between the predicted and target values. The words residual and skip are used interchangeably in many places. They can also be thought of as an identity block. If there is no residual then H(x) = x (aka the identity).
A residual block is trying to learn the residual of the true distribution minus the input, while a normal layer tries to learn that true distribution
why does this work better?
Theoretically this shouldn’t matter. Neural networks are function approximations. The more layers you add, the better the approximation should be. However, this does not work in reality for many reasons such as exploding or vanishing gradients. By allowing the values to essentially pass through in a linear way, we can use previous gradients.
In other words, a deeper net is not necessarily optimal because it might not learn the abstractions as the information learned in the earlier layers might disappear in the later layers.
Less layers means a simpler model which is faster to train.
code
class ResidualBlock(nn.Module):
expansion = 1
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion*planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion*planes, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion*planes)
math
R(x) is the residual
H(x) is the output aka true distribution
x is the input in the layer
R(x) = Output — Input = H(x) — x
The residual plus the input is the true distribution
H(x) = R(x) + x
history
First introduced by microsoft in 2015.