In this post, I will introduce the direction of my OpenAI scholars’ project.
Inspired by the Scaling Laws papers by OpenAI on language models, and autoregressive models published last year, I’m interested in learning more about exploring potential scaling laws for dataset complexity. The questions I’m most interested in studying with my project are: Are there universal scaling laws for dataset complexity, or is dataset difficulty more of a pre-factor to performance? Another way to phrase this would be, can we build a map of scaling laws with respect to dataset complexity for regular languages? Can we show that these same trends apply to other natural datasets if there are scaling relationships for dataset complexity for regular languages?
Finding scaling laws for dataset complexity will contribute to a more precise understanding of transformer models and data. There exists substantial literature on the impact of algorithms and compute for machine learning, but less on the impact of data on machine learning. Previous scaling laws work has shown the relationship between dataset size and model performance. However, other potential relationships that may exist with data have not yet been explored. Understanding datasets may provide insights on how to improve performance on downstream tasks, in addition to how to transfer unsupervised approaches with transformers to other domains of ML research.
Yet while neural networks have made incredible progress, it is not always clear why this progress has been made. Better understanding what factors, such as dataset complexity, are causing models to work and why they are improving will allow us to better predict which capabilities will develop and when.
What is a Regular Language?
I will train transformers to predict the next character for strings from a regular language for my experiments. A regular language is a type of formal language defined by a regular expression. Formal language is a set of words from a given finite alphabet. Kleene’s theorem shows finite automata and regular expressions are equivalent in their expressiveness for denoting languages.
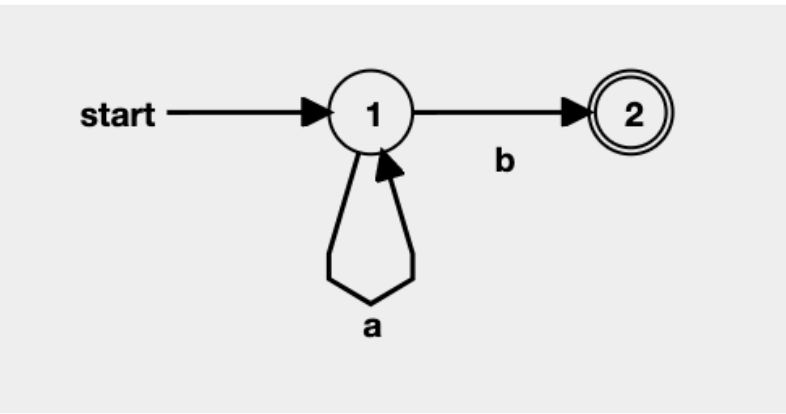
For example, the regular expression a*b can convert into a non-deterministic finite automaton (NFA), which can convert into a deterministic finite automaton (DFA), which can reduce into a minimum deterministic finite automaton (MDFA). It has two states, with one of those states being an accepting or final state.
The symbols of the regular language a*b are a and b, and it has two transitions. A string is a valid word in a given language if it ends in an accepting state of the finite automaton representing the language.
Measuring Complexity
To measure dataset complexity, we will compare the number of states, transitions, and end states of the deterministic finite automata against the different regular languages. The number of states is the primary number of comparisons. The thesis here is that more states would result in a more complicated language. However, it is also essential to consider the secondary factors, such as how many states are accepting stages and how many transitions are between the states. For example, a finite automaton with many states, but all of the states are accepting, will be easy to solve. The advantages of using our synthetic languages will allow us to build a formal measurement of complexity. Creating a formal measure of complexity will allow us to increase the difficulty and control our data. For example, we can generate as many samples as needed and will not be data limited. There is existing research in computer science for how to measure the complexity of regular languages such as state complexity, and quotient complexity.
Progress So Far
Currently, I have been testing GPT and TransformerXL architectures on generated datasets of various regular languages. It appears that the number of transitions in the finite automaton impacts how easy a language is to learn. I started off generating datasets of 50> states with 100+ transitions but found that the models could not learn anything. I had initially been worried that creating straightforward regular languages would not be interesting to study. I’ve since been working from very simple (but still infinite) regular languages and plan on slowly increasing the number of states and transitions.
Thanks to my mentor Jerry Tworek for helping me design this project!